When I read Machine Learning papers, I ask myself whether the contributions of the paper fall under improvements to 1) Expressivity 2) Trainability, and/or 3) Generalization. I learned this categorization from my colleague
. I have found this categorization effective in thinking about how individual research papers (especially on the theoretical side) tie subfields of AI research (e.g. robotics, generative models, NLP) together into one big picture [1].
In this blog post, I discuss how these concepts tie into current (Nov 2017) machine learning research on Supervised Learning, Unsupervised Learning, and Reinforcement Learning. I consider Generalization to be comprised of two categories -- “weak” and “strong” generalization -- and I will discuss them separately. This table summarizes my opinion on where things are:
This post covers a broad spectrum of research at a fairly opinionated level. I emphasize that any factual errors here are my own and do not reflect opinions of my colleagues and proofreaders. Feel free to contribute feedback in the comments or send me an email if you’d like to discuss / suggest edits - I’m here to learn.
Expressivity
What computations can this model perform?
Measures of expressivity characterize the complexity of functions that can possibly be computed by a parametric function such as a neural net. Deep neural networks are exponentially
expressive with respect to their depth, which means that moderately-sized neural networks are sufficiently expressive for most supervised, unsupervised, and RL problems being researched today [2]. One piece of evidence for this is that deep neural nets are capable of
memorizing very large datasets.
Neural nets can express all sorts of things: continuous, complex, discrete, and even stochastic variables. Thanks to research in generative modeling and
Bayesian Deep Learning in the last few years, deep neural networks have been leveraged to construct probabilistic neural networks have produced incredible generative modeling results.
Recent breakthroughs in generative modeling illustrate the profound expressivity of neural networks: neural nets can output extremely complex data manifolds (audio, images) that are
nearly indistinguishable from real data. Here is the output on a recent
GAN architecture proposed by researchers at NVIDIA:


It’s not perfect yet (notice the warped background), but we are getting very close. Similarly, in audio synthesis, generated audio samples from the latest WaveNet models
sound like real people.
Unsupervised learning is not limited to generative modeling. Some researchers like Yann LeCun are rebranding unsupervised learning as “predictive learning”, where the model infers the past, imputes the present, or predicts the future. However, since much of unsupervised learning has focused on predicting extremely complex joint distributions (images from past/future, audio), I think generative modeling is a reasonably good benchmark to measure expressivity in the unsupervised domain.
Neural nets seem to be expressive enough for RL as well. Fairly small networks (2 conv layers and 2 fully-connected layers) are powerful enough to solve
Atari and MuJoCo control tasks (though their trainability leaves much to be desired - see the next section).
On its own, expressivity is not a very interesting question - we can always increase it by adding more layers, more connectivity, and so on. The challenge is making neural nets expressive enough for both the training and test set, while keeping the training difficulty manageable. For example, 2D convolutions seem to be required to make image classification models generalize, even though a deep fully-connected network has enough capacity to memorize a training set.
Expressivity is the easiest problem to deal with (add more layers!), but also simultaneously the most mysterious: we don’t have a good way of measuring how much expressivity (and of what kind) is demanded by a given task. What kinds of problems will demand neural networks that are orders of magnitude larger than the ones we use today? Why will they require so much compute? Are our current neural networks expressive enough to implement intelligence resembling that of a human? Does solving generalization on much harder problems require vastly more expressive models?
The brain has many orders of magnitude more “neuronal units” (1e11) than the number of units in our large neural networks (Inception-ResNet-V2 has roughly 25e6 ReLU units). This comparison is already drastic, even when we give ReLUs the benefit of the doubt that they are even remotely comparable to biological neurons. A single biological neuron -- with its various neurotransmitters, dendritic forest integrating input from 10000 other neurons in a time-varying integration -- is also incredibly expressive. A locust implements its collision detection system in one neuron and it already flies better than any drone system we have ever built. Where is all this expressivity coming from and going to? How much more expressivity do we need?
Trainability
Given a sufficiently expressive space of models, can we find a good model?
A Machine Learning model is any computer program that has some of its functionality learned from data. During “learning”, we search for a reasonably good model that utilizes knowledge from the data to make decisions, out of a (potentially huge) space of models. This search process is usually formulated as solving an optimization problem over the space of models.

Several Varieties of Optimization
A common approach, especially in deep learning, is to define some scalar metric that evaluates the “goodness” of a model. Then use a numerical optimization technique to maximize said “goodness” (or equivalently, “minimize badness”).
A concrete example: minimizing the average cross-entropy error is a standard way to train neural networks to classify images. This is done in the hopes that when the model with dataset have been minimized on cross entropy loss, it will also do what we actually want, e.g. classify images correctly with a certain degree of precision and recall on test images. Often the evaluation metric cannot be optimized directly (the most obvious reason being that we don’t have access to the test dataset) but a surrogate function like cross-entropy on a training set can.
Searching for good models (training) ultimately amounts to optimization -- no two ways about it! But … objectives are sometimes hard to specify. A classic scenario in supervised learning is in image down-sampling, where it’s difficult to define a single scalar quantity that aligns exactly with how humans perceive “perceptual loss” from a particular downsampling algorithm. In a similar manner, super-resolution and image synthesis are also difficult, because we have a hard time writing down the “goodness” as a maximization objective. Imagine writing down a function that tells you how “photoreal” an image is! The debate on how to measure quality of generative models (for images, audio)
rages on to
this day.
The most popular technique in recent years that addresses this problem is a co-adaptation approach, which formulates the optimization problem as solving for the equilibrium point between two non-stationary distributions that are evolving in tandem [3]. An intuitive analogy to explain why this is “natural” would be to compare this to ecological evolution of a predator species and a prey species. At first, predators get smarter so they can catch prey effectively. Then, the prey get smarter in order to evade predators. The species co-evolve against each other, and the end result is that both species become more intelligent.
Generative Adversarial Networks operate according to a similar principle, in order to avoid having to define explicit perceptual loss objectives. Similarly, competitive self-play in reinforcement learning employs this principle to learn
rich behaviors. Although the optimization objective is now implicitly specified, it’s still an optimization problem, and machine learning practitioners can re-use familiar tools like deep neural networks and SGD.
Evolution strategies typically consider optimization-as-a-simulation. The user specifies some dynamical system over a population of models, and at each timestep of the simulation, the population is updated according to the rules of the dynamical system. The models may or may not interact with each other. The simulation runs forward in time, and hopefully the dynamics of the system induce the population to eventually converge around “good models”.
For a great tutorial on ES in the context of RL, see
A Visual Guide to Evolution Strategies by David Ha (the “References and Further Reading” section is really great!).
Current State of Affairs
Trainability is basically solved for feedforward networks and “direct” objectives encountered in supervised learning (I make this claim empirically, not theoretically). Some popular breakthroughs published in 2015 (
Batch Norm,
ResNets,
Good Init) are widely used today to make training of feedforward networks super trainable. In fact, deep nets with hundreds of layers can now minimize
training error of large classification datasets to zero. See
this paper for a comprehensive survey on the hardware and algorithmic infrastructure underlying modern DNNs.
RNNs are still pretty tricky, but the research community is making a lot of progress, to the point where it is no longer crazy to
drop an LSTM into a complex robotic policy and expect it to “just work”. That’s pretty incredible, considering that as late as 2014 not many people had confidence in trainability RNNs and in the previous decades there was a
lot of
work showing that RNNs are horrible to train. There’s evidence that a whole bunch of RNN architectures are
equivalently expressive, and any differences in performance are due to some architectures being
easier to optimize than others [4].
In unsupervised learning, the model outputs are often (but not always!) bigger -- for instance, 1024 x 1024 pixels, gigantic sequences for speech and text. This unfortunately makes them harder to train.
One of the big breakthroughs in 2017 was that GANs are now dramatically easier to train. The most popular improvements have been simple modifications to the original Jensen-Shannon divergence objective:
least squares,
absolute deviation with margin, and Wasserstein distance (
1,
2). The
recent work by NVIDIA extends Wasserstein-based GANs to be make the model less sensitive to a wide variety of hyperparameters like BatchNorm parameters, architecture choice, and so on. Stability is incredibly important for practical and industrial applications - it’s what gives us the confidence that it will be compatible with our future research ideas or applications. Taken together, these results are exciting because they indicate that our generator neural networks are plenty expressive to generate the right images, and the bottleneck that was holding them back was one of trainability. Trainability might still be a bottleneck - unfortunately with neural nets it’s hard to tell if a model is simply not expressive enough and/or we haven’t trained it enough.
Latent discrete variable inference within neural nets was also previously difficult to train due to monte-carlo gradient estimators having high variance. However it’s starting to make a comeback in recent years in all sorts of architectures, from GANS to Language Modeling to Memory-Augmented Neural Networks to Reinforcement Learning. Discrete representations are very useful from an expressivity standpoint and it’s great that we can now train them
fairly reliably.
Tragically, Deep Reinforcement Learning is still quite behind when it comes to pure trainability, without even considering the generalization aspect. Reinforcement learning is difficult because for environments with more than 1 timestep, we are searching for a model that then performs optimization (of the reward) at inference time. There is an inner optimization process where the model induces optimal control, and an outer optimization loop that learns this optimal model, using only a database of what the agent saw.
Recently I added one extra dimension to a continuous robotic control task, and the performance of my RL algorithm dropped from >80% to 10%. Not only is RL training hard, but it’s also unreliable! Because optimization landscapes are so stochastic, we can’t even get the same results with
different random seeds, so the strategy is to report a distribution of reward curves over multiple trials, with different random seeds. Different implementations of the same algorithm perform differently across environments, so RL scores reported in literature are to be taken with a handful of salt.
This is a travesty! Trainability in RL is still very much unsolved, because we still cannot scale up our problems by a little bit and expect the same learning to do the same thing 10 times out of 10.
If we treat RL as a pure optimization problem (and worry about generalization and complex tasks later), the problem is still intractable. Let’s say there’s an environment where a sparse reward is given only at the end of the episode (e.g. babysitting a child where the babysitter is paid after the parents return home). The number of actions (and corresponding outcomes of the environment) grows exponentially with the duration of the episode, but only a few of these action sequences corresponds to a success.
Therefore, estimating the policy gradient at any point in the optimization landscape of models requires exponentially many samples in the action space before a useful learning signal is obtained. This is as bad as trying to compute a Monte Carlo expectation of a probability distribution (over all action sequences) where the mass is concentrated at a “dirac delta distribution” (see diagram below). When there is vanishing overlap between the proposal distribution (exploration) and reward distribution, finite-sample Monte Carlo estimates of policy gradients simply will not work, no matter how many samples you collect.
Furthermore, if the data distribution is non-stationary (as in the case of off-policy learning algorithms with a replay buffer), collecting “bad data” can introduce unstable feedback loops into the outer optimization process.
Here’s the same idea from an optimization perspective rather than a Monte Carlo estimation perspective: without any priors over the state space (such as an understanding of the world or an explicit instruction provided to the agent), the optimization landscape looks like “swiss cheese” -- small “holes” of convex optima surrounded by vast plateaus of parameter space where policy gradient information is useless. This means that the entire model space basically has zero information (because the learning signal is effectively uniform across the space of models, since the non-zero area is vanishingly small).

Without developing good representations that we can do learning on top of, we might as well just cycle through random seeds and sample random policies until we happen upon a good model that lands in one of these swiss cheese holes. The fact that this is a surprisingly strong baseline in RL suggests that our optimization landscapes may very well look like this.
I believe that RL benchmarks like Atari and MuJoCo, while interesting from a pure optimization standpoint, do not really push the limits of machine learning, so much as just solve for a single monolithic policy that optimizes performance for a fairly sterile environment. There is little selective pressure encouraging the model to “generalize”, which makes the problem a pure optimization problem, and not really a hard ML problem.
Thinking about generalization in RL (and not just trainability) makes things much harder to interpret and debug, but I think learning understanding of the environment and understanding the task is the only way that will make reinforcement learning tractable for real-world robotic problems.
Contrast this with supervised learning and unsupervised learning, we can obtain learning signals cheaply, no matter where we are in the model search space. The proposal distribution for minibatch gradients has nonzero overlap with the distribution of gradients. If we are using SGD with minibatch size=1, then the probability of sampling the transition with a useful learning signal is at worst 1/N where N is the size of the dataset (so learning is guaranteed after each epoch). We can brute-force our way to a good solution by simply throwing a lot of compute and data at the problem. Furthermore, improving perceptual generalization of lower layers may actually have a variance-reducing effect via “bootstrapping” on top of lower-level features.
In order to solve RL problems with high dimensionality and complexity, we must consider generalization and general perceptual understanding before tackling the numerical optimization problem. To attempt otherwise is a foolish waste of compute and data (though it’s still useful to answer exactly how much we can brute force). We need to get to a point where every data point provides a non-zero number of bits to the RL algorithm, and have an easy way to importance-sample gradients when the task is very complex (without gathering exponentially more data). Only then, is it reasonable to assume we can succeed at brute-forcing the problem.
Learning from demonstration, imitation learning, inverse reinforcement learning, and interfacing with natural language instructions perhaps provide ways to quickly bring the starting policy to a point that obtains some learning signal, or shape the search space in a way such that each episode gives a non-zero amount of information to the policy (for example, the environment provides a reward of 0 but observations yield some information that is helpful to the inductive biases of the model’s planning module).
To summarize: trainability is: easy for supervised learning, is harder-but-getting-there for unsupervised learning, and is still terribly broken for reinforcement learning.
Generalization
Generalization is the most profound of the 3 problems, and is the heart of Machine Learning itself. Loosely speaking, it is how well the model performs on test dataset when it is trained on a training dataset.
There are two distinctive scenarios when talking about generalization: 1) the training and test data are sampled from the same distribution (and we need to learn this distribution from the training data alone) or 2) training and test data are drawn from different distributions (and we need to generalize from the train to the test distribution). Let’s call (1) “weak generalization” and (2) “strong generalization. This way of classifying generalization could be also referred to as “interpolation vs. extrapolation”, or “robustness vs. understanding”.
Weak Generalization: Two Landscapes
How well does the model perform on small perturbations of its data distribution?
In “weak generalization”, we usually assume the training and test data samples are drawn from the same distribution. However, in real world settings, there is almost always some difference between the train and test distributions, even in the large-sample limit.
These differences can come from sensor noise, changes in ambient light conditions, gradual wear and tear of objects, variations in lighting conditions (maybe it was a cloudy day when the photographer gathered the test set images). Another situation is that differences can be
generated by an adversary. Adversarial perturbations are barely perceptible to our human vision, so we might consider adversarial examples to be drawn from the “same distribution”.
Therefore, it’s helpful in practice to think about “weak generalization” as evaluating on a “perturbed” version of the training distribution:

A perturbed testing data distribution might also induce a perturbed optimization landscape (lowest point is best).
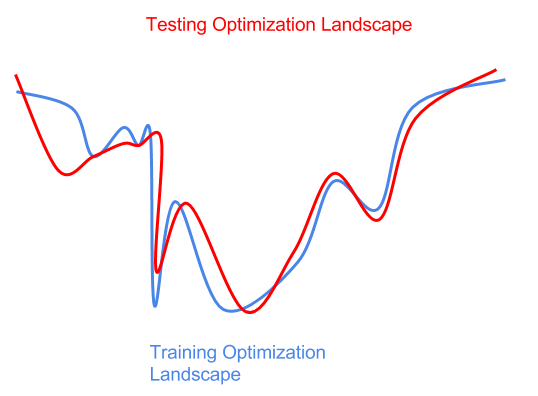
The fact that we don’t know the testing distribution ahead of time presents some difficulties for optimization. If we are too aggressive in optimizing the training landscape (the sharp global minima on the left of the blue curve), we end up with a model that is sub-optimal with respect test data (sharp local minima on the red curve). Here, we’ve overfit to the training distribution or training data samples, and failed to generalize to the perturbed test distribution.
“Regularization” is any technique we employ to prevent overfitting. We don’t have any prior information on what the test perturbation is, so often the best we can usually do is try to train on random perturbations versions of the training distribution, in hopes that these perturbations cover the test distribution. Stochastic gradient descent, dropout, weight noise, activation noise, data augmentation are commonly-used regularizers in Deep Learning. In reinforcement learning, randomizing simulation parameters makes the training more robust. In his talk at ICLR 2017, Chiyuan Zhang made the comment that he sees regularization as “anything that makes training harder” (rather than the conventional view of “limiting model capacity”). Basically, making things *harder* to optimize somehow improves generalization.
This is really disturbing -- our methods of “generalizing” are quite crude, amounting to “optimizer lobotomy”. We basically throw a wrench into the optimizer and hope it messes training just enough to prevent overfitting. Furthermore, improving trainability is can make you pay a price in generalization! This way of viewing (weak) generalization certainly complicates how we proceed with trainability research.
But if better optimizers overfit, then how do we explain why some optimizers seem to decrease both training and test error? The reality is that any combination of optimization landscape and optimizer strikes a balance between 1) finding a better region of models and 2) overfitting to a specific solution, and we don’t have good methods for controlling this balance.
The most challenging test of weak generalization is probably that of adversarial attacks, where the perturbations are coming from an “adversary” that provides the worst-possible perturbation to your data point, so that your model performs badly with high probability. We still don’t have any deep learning approaches that are very
robust to adversarial examples, but my gut feeling is that it is eventually solvable [5].
There’s some theoretical work on applying information theory to show that neural networks apparently go through a phase transition during the training process in which the model
switches from “memorizing” data to “compressing” data. This theory is starting to pick up steam, though there is ongoing academic debate as to
whether this theory is valid. Keep your eyes peeled for this one - the intuition of “memorization” and “compression” is compelling.
Strong Generalization: Natural Manifold
In tests of “strong generalization”, the model is evaluated on a completely different data distribution than the test, but with data coming from the same underlying manifold (or generative process).

How could one could ever learn a good model for the test distribution if it is “completely different” from the training distribution? The resolution for this is that these “glimpses” of data actually come from the same manifold of “natural data”. There can still be a lot of information overlap between train and test distributions, as long as they come from the same underlying generative process.
The space of observable data in the world can be described as a very high-dimensional, continuously varying “natural manifold”. The tuple (video clip of a pair of cymbals crashing together, the sound of crashing cymbals) is a point on this manifold. The tuple (video clip of a pair of cymbals crashing together, the sound of frogs croaking)is not - those joint data points are simply are inconsistent with our reality. As you can see, even though the manifold is positively gigantic, it’s also highly structured. For example, physical laws like gravity are obeyed in all the data that we observe, objects don’t blip in and out of existence, and so on.
Strong Generalization can be thought of as how much of this “super-manifold” is captured by a particular model that is only trained on a teensy sampling of data points from the manifold. Note that an image classifier does not need to discover Maxwell’s Equations -- it merely needs to have an understanding of reality that is consistent with data on the manifold.
Modern classification models trained on ImageNet are arguably OK at strong generalization - principles like edges, contours, and objects are indeed understood by models trained on ImageNet, which is why it’s so popular to transfer these pre-trained weights to other datasets for few-shot & metric learning. It could be a lot better though: classifiers trained on ImageNet don’t work universally, few-shot learning still is unsolved, and they are still susceptible to adversarial examples. Obviously our models don’t understand what they are looking at, to the same degree that humans do. But
it’s a start.
Similar to weak generalization, the test distribution can be sampled adversarially in a way that induces maximum discrepancy between the training and testing distribution. AlphaGo Zero is my favorite example of this: at test time, it observes data from human players that is completely different than its training distribution (it has never “seen” a human before). Furthermore, the human is using all of their intelligence to actively lead AlphaGo to regimes that are unobserved in the training data. Even though AlphaGo doesn’t explicitly understand anything about abstract mathematics, opponent psychology, or what the color green means, it clearly understood enough about the world to outwit a human player within a narrow domain. If an AI system is robust against a skilled human adversary, I consider it to have sufficient strong generalization capability.
Sadly, Reinforcement Learning research has largely ignored the problem of strong generalization. Most benchmarks are static environments, with very little perceptual richness (e.g. the humanoid doesn’t understand its world or what its body even looks like, beyond some floating joint positions that lead to some reward).
I really believe that solving generalization is key to solving RL trainability. The more our learning system “understands” about the world, the better able it is to obtain learning signals, perhaps with fewer samples. This is why few-shot learning, imitation learning, learning-to-learn is important: it moves us away from brute force solutions where variance is high and information is low.
I believe two things are required to achieve stronger forms of generalization:
First, we need models that actively deduce the fundamental laws of the world from observation and experimentation. Symbolic reasoning and
causal inference seem like ripe topics to study, but any kind of unsupervised learning is likely to help. I am reminded of humankind’s long quest to understand the motion of celestial bodies by deriving physical laws of the universe using a system of logical reasoning (mathematics). It’s interesting to note that before the
Copernican Revolution humans probably relied on Bayesian heuristics at first (“superstitions”), and these “Bayesian” models were discarded once we discovered classical mechanics.
Our model-based machine learning methods (models that attempt to “predict” aspects of their environment) right now are “pre-Copernican” in the sense that they only interpolate based on very shallow statistical superstitions, rather than coming up with deep, general principles to explain and extrapolate data that can be millions of light years away or many timesteps into the future. Note that humans didn’t really need a firm grasp on probability theory to derive deterministic celestial mechanics, which begs the question of whether there are ways to do machine learning and causal inference without an explicit statistical framework.
One way to drastically reduce the complexity burden is to make our learning systems more adaptive. We need to go beyond optimizing models that predict or act in static ways. Instead, we need to be optimizing models that can think, remember, and learn, all in real-time.
Second, we need to throw enough diversity of data at the problem, so that the model can be pushed to develop these abstract representations. An environment needs to be rich enough to force the right representations to develop (though AlphaGo Zero does raise questions on how much of the natural manifold an agent really needs to experience). Without these constraints, the problem is fundamentally underspecified and the chance that we accidentally discover the right solution is nil. Perhaps humans would never have gained intelligence if they could not stand up on their hind legs and wonder about why stars moving in such
strange, elliptical patterns.
I wonder if the Trisolarian civilization (from the book "The Three Body Problem") evolved to such a high level of technological advancement because their livelihoods depended on their physical understanding of complex celestial mechanics. Maybe we need to introduce some celestial motion into our Mujoco & Bullet environments :)
Footnotes
[1] There are some research areas that don’t fit as neatly into the framework of expressivity, trainability, and generalization. For example, interpretability research seeks to understand why a model provides a particular answer. Not only is this expected by ML customers and policymakers in some high-stakes fields (medicine, law enforcement), but these can shed light on generalization: if we discover that the model is providing diagnoses in a way that differs a lot from how a human medical professional would arrive at those conclusions, it could mean that there are edge cases where the model’s deductive process will fail to generalize. Finding out whether your model learned the right thing is even stronger having low test error! Differential privacy is another constraint that we sometimes demand from our ML models. These topics are out of the scope of this blog post.
[2] A hand-wavy explanation for why this is the case: A fully-connected layer of size N followed by a ReLU nonlinearity can chop up a vector space into N piecewise-linear pieces. Adding a second ReLU layer further subdivides space into N more pieces, resulting in N^2 piecewise linear regions in input space, 3 layers is N^3, and so on. For detailed analysis, see Raghu et al. 2017.
[3] This is sometimes called a
Multi-level optimization problem. However, this implies an “outer” and “inner” optimization loop, whereas co-adaptation may occur simultaneously. e.g. concurrent processes on a single machine communicating asynchronously, or species evolving continuously w.r.t each other in an ecosystem. In these cases, there is no clear “outer” and “inner” optimization loop.
[4]
seq2seq with attention achieved SOTA when they were first introduced, but I suspect that the advantage it confers is one of trainability, not expressivity or generalization. Maybe seq2seq without attention can do just as well if it is properly initialized.
[5] One idea to protect against adversarial methods, without solving strong generalization: make it extremely expensive to compute adversarial perturbations. Models and data are partially black-box. At each call to the model during inference time, randomly pick a model from an ensemble of trained models, and serve that model to the adversary without telling them which model they got. The models are trained independently of each other and can even adopt different architectures. This makes it difficult to compute finite-difference gradients, as f(x+dx) - f(x) can have arbitrarily high variance. Furthermore, gradients between successive gradient computations will still have high variance because different pairs of models can be sampled. Another way to improve things would be to use multi-modal data (video, multi-view, images + sound), so that it is difficult to perturb inputs in a way that preserves consistency of inputs.







